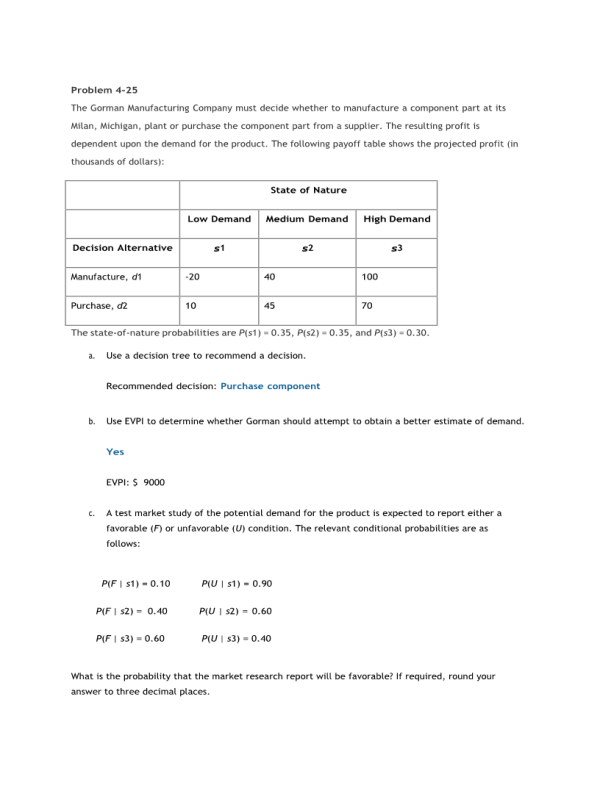
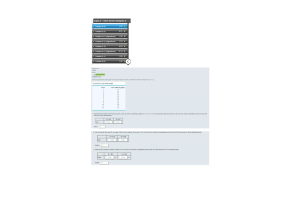
Problem 4-25: The Gorman Manufacturing Company must decide whether to manufacture a component part at its Milan, Michigan, plant or purchase the component part from a supplier. The resulting profit is dependent upon the demand for the product. The following payoff table shows the projected profit (in thousands of dollars):

The state-of-nature probabilities are P(s1) = 0.35, P(s2) = 0.35, and P(s3) = 0.30.

1. Use a decision tree to recommend a decision.
2. Use EVPI to determine whether Gorman should attempt to obtain a better estimate of demand.
3. A test market study of the potential demand for the product is expected to report either a favorable (F) or unfavorable (U) condition. The relevant conditional probabilities are as follows:

What is the probability that the market research report will be favorable? If required, round your answer to three decimal places.

4. What is Gorman's optimal decision strategy?
5. What is the expected value of the market research information?

Problem 4-17: Hemmingway, Inc., is considering a $5 million research and development (R&D) project. Profit projections appear promising, but Hemmingway's president is concerned because the probability that the R&D project will be successful is only 0.50. Furthermore, the president knows that even if the project is successful, it will require that the company build a new production facility at a cost of $20 million in order to manufacture the product. If the facility is built, uncertainty remains about the demand and thus uncertainty about the profit that will be realized. Another option is that if the R&D project is successful, the company could sell the rights to the product for an estimated $25 million. Under this option, the company would not build the $20 million production facility. The decision tree is shown in Figure 4.16. The profit projection for each outcome is shown at the end of the branches. For example, the revenue projection for the high demand outcome is $59 million.

However, the cost of the R&D project ($5 million) and the cost of the production facility ($20 million) show the profit of this outcome to be $59 − $5 − $20 = $34 million. Branch probabilities are also shown for the chance events.

1. Analyze the decision tree to determine whether the company should undertake the R&D project. If it does, and if the R&D project is successful, what should the company do?

What is the expected value of your strategy?

2. What must the selling price be for the company to consider selling the rights to the product? Payoff for sell rights would have to be $25M or more. In order to recover the $5M R&D cost, the selling price would have to be $ 30M or more.
3. Develop a risk profile for the optimal strategy. If required, round your answers to two decimal places.

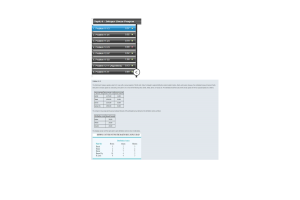
Problem 4-23 (Algorithmic)

Suppose that you are given a decision situation with three possible states of nature: S1, S2, and S3. The prior probabilities are P(S1) = 0.20, P(S2) = 0.50, and P(S3) = 0.30. With sample information I, P(I | S1) = 0.10, P(I | S2) = 0.05, and P(I | S3) = 0.20. Compute the revised or posterior probabilities: P(S1 | I), P(S2 | I), and P(S3 | I). If required, round your answers to four decimal places.

Problem 4-05 (Algorithmic)

In American football, touchdowns are worth 6 points. After scoring a touchdown, the scoring team may subsequently attempt to score 1 or 2 additional points. Going for 1 point is virtually an assured success, while going for 2 points is successful only with probability p. Consider the following game situation. The Temple Wildcats are losing by 14 points to the Killeen Tigers near the end of regulation time. The only way for Temple to win (or tie) this game is to score two touchdowns while not allowing Killeen to score again. The Temple coach must decide whether to attempt a 1-point or 2-point conversion after each touchdown. If the score is tied at the end of regulation time, the game goes into overtime. The Temple coach believes that there is a 42% chance that Temple will win if the game goes into overtime. The probability of successfully converting a 1-point conversion is 1.0. The probability of successfully converting a 2-point conversion is p.

1. Assume Temple will score two touchdowns and Killeen will not score. Create a decision tree for the decision of whether Temple's coach should go for a 1-point conversion or a 2-point conversion after each touchdown. The terminal nodes in the decision tree should be either WIN or LOSE for Temple.

b. Assume that a WIN results in a value of 1.0 and LOSE results in a value of 0. Further, assume that the probability of converting a 2-point conversion is p = 35%. Should Temple's coach go for a 1-point conversion or 2-point conversion after scoring the first touchdown?

Problem 4-11 (Algorithmic)

Following is the payoff table for the Pittsburgh Development Corporation (PDC) Condominium Project. Amounts are in millions of dollars.

Suppose PDC is optimistic about the potential for the luxury high-rise condominium complex and that this optimism leads to an initial subjective probability assessment of 0.81 that demand will be strong (S1) and a corresponding probability of 0.19 that demand will be weak (S2). Assume the decision alternative to build the large condominium complex was found to be optimal using the expected value approach. Also, a sensitivity analysis was conducted for the payoffs associated with this decision alternative. It was found that the large complex remained optimal as long as the payoff for the strong demand was greater than or equal to $18.05 million and as long as the payoff for the weak demand was greater than or equal to -$13.05 million.

1. Consider the medium complex decision. How much could the payoff under strong demand increase and still keep decision alternative d3 the optimal solution? If required, round your answer to two decimal places.
2. Consider the small complex decision. How much could the payoff under strong demand increase and still keep decision alternative d3 the optimal solution? If required, round your answer to two decimal places.

Problem 4-07

Hudson Corporation is considering three options for managing its data processing operation: continuing with its own staff, hiring an outside vendor to do the managing (referred to as outsourcing), or using a combination of its own staff and an outside vendor. The cost of the operation depends on future demand. The annual cost of each option (in thousands of dollars) depends on demand as follows:

1. If the demand probabilities are 0.2, 0.5, and 0.3, which decision alternative will minimize the expected cost of the data processing operation?

What is the expected annual cost associated with that recommendation?

2. Construct a risk profile for the optimal decision in part (a).

The input in the box below will not be graded, but may be reviewed and considered by your instructor.

What is the probability of the cost exceeding $700,000? If required, round your answer to two decimal places.

Problem 4-15

The Lake Placid Town Council decided to build a new community center to be used for conventions, concerts, and other public events, but considerable controversy surrounds the appropriate size. Many influential citizens want a large center that would be a showcase for the area. But the mayor feels that if demand does not support such a center, the community will lose a large amount of money. To provide structure for the decision process, the council narrowed the building alternatives to three sizes: small, medium, and large. Everybody agreed that the critical factor in choosing the best size is the number of people who will want to use the new facility. A regional planning consultant provided demand estimates under three scenarios: worst-case, base-case, and best-case. The worst-case scenario corresponds to a situation in which tourism drops substantially; the base-case scenario corresponds to a situation in which Lake Placid continues to attract visitors at current levels; and the best-case scenario corresponds to a substantial increase in tourism. The consultant has provided probability assessments of 0.10, 0.60, and 0.30 for the worst-case, base-case, and best-case scenarios, respectively.

The town council suggested using net cash flow over a 5-year planning horizon as the criterion for deciding on the best size. The following projections of net cash flow (in thousands of dollars) for a 5- year planning horizon have been developed. All costs, including the consultant's fee, have been included.

1. What decision should Lake Placid make using the expected value approach?
2. Identify the risk profiles for the medium and large alternatives. Risk profile for medium-size community center: Graph (ii) Risk profile for large-size community center: Graph (iii)
3. Compute the expected value of perfect information.

Do you think it would be worth trying to obtain additional information concerning which scenario is likely to occur?

4. Suppose the probability of the worst-case scenario increases to 0.2, the probability of the base- case scenario decreases to 0.5, and the probability of the best-case scenario remains at 0.3. What effect, if any, would these changes have on the decision recommendation?
5. The consultant has suggested that an expenditure of  $150,000  on a  promotional  campaign over the planning horizon will effectively reduce the probability of the worst-case scenario to zero. If the campaign can be expected to also increase the probability of the best-case scenario to 0.4, is it a good investment?

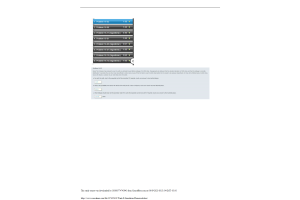
Problem 4-21 (Algorithmic)

A real estate investor has the opportunity to purchase land currently zoned residential. If the county board approves a request to rezone the property as commercial within the next year, the investor will be able to lease the land to a large discount firm that wants to open a new store on the property.

However, if the zoning change is not approved, the investor will have to sell the property at a loss. Profits (in thousands of dollars) are shown in the following payoff table:

1. If the probability that the rezoning will be approved is 0.5, what decision is recommended?

What is the expected profit?

2. The investor can purchase an option to buy the land. Under the option, the investor maintains the rights to purchase the land anytime during the next three months while learning more about possible resistance to the rezoning proposal from area residents. Probabilities are as follows:

What is the optimal decision strategy if the investor uses the option period to learn more about the resistance from area residents before making the purchase decision?

3. If the option will cost the investor an additional $10,000, should the investor purchase the option?
4. What is the maximum that the investor should be willing to pay for the option?