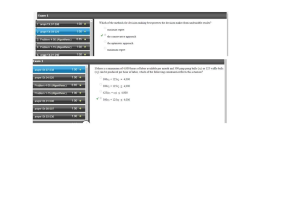
1. Question: A company makes two products from steel; one requires 2 tons of steel and the other requires 3 tons. There are 100 tons of steel available daily. A constraint on daily production could be written as: 2x₁ + 3x₂ ≤ 100.
2. Question: Let x₁ , x₂ , and x₃ be 0 - 1 variables whose values indicate whether the projects are not done (0) or are done (1). Which answer below indicates that at least two of the projects must be done?
3. Question: The constraint x₁ + x₂ + x₃ + x₄ ≤ 2 means that two out of the first four projects must be selected.
4. Question: Each point on the efficient frontier graph associated with the Markowitz portfolio model is the
5. Question: Consider a maximal flow problem in which vehicle traffic entering a city is routed among several routes before eventually leaving the city. When represented with a network,
6. Question: Assuming W₁, W₂ and W₃ are 0 -1 integer variables, the constraint W₁ + W₂ + W₃ < 1 is often called a
7. Question: Let M be the number of units to make and B be the number of units to buy. If it costs $2 to make a unit and $3 to buy a unit and 4000 units are needed, the objective function is
8. Question: The dual price for a constraint that compares funds used with funds available is .058. This means that
9. Question: Problem 9-11 (Algorithmic): Edwards Manufacturing Company purchases two component parts from three different suppliers. The suppliers have limited capacity, and no one supplier can meet all the company’s needs. In addition, the suppliers charge different prices for the components. Component price data (in price per unit) are as follows:

Each supplier has a limited capacity in terms of the total number of components it can supply. However, as long as Edwards provides sufficient advance orders, each supplier can devote its capacity to component 1, component 2, or any combination of the two components, if the total number of units ordered is within its capacity. Supplier capacities are as follows:

If the Edwards production plan for the next period includes 1025 units of component 1 and 825 units of

component 2, what purchases do you recommend? That is, how many units of each component should be ordered from each supplier?

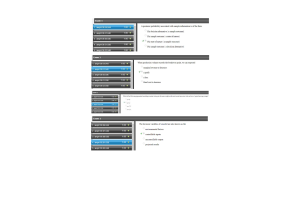
10. Question: To develop a portfolio that provides the best return possible with a minimum risk, the linear programming model will have an objective function which
11. Question: The total cost for a waiting line does NOT specifically depend on
12. Question: The media selection model presented in the textbook involves maximizing the number of potential customers reached subject to a minimum total exposure quality rating.
13. Question: Let P_ij = the production of product i in period j. To specify that production of product 1 in period 3 and in period 4 differs by no more than 100 units,
14. Question: The number of units shipped from origin i to destination j is represented by
15. Question: Problem 15-09 (Algorithmic) Mart’s barber shop has one barber. Customers have an arrival of 2.2 customers per hour,……
16. Question: The assumption that arrivals follow a Poisson probability distribution is equivalent to the assumption that the time between arrivals has
17. Question: If arrivals occur according to the Poisson distribution every 20 minutes, then which is NOT true?
18. Question: The overall goal of portfolio models is to create a portfolio that provides the best balance between
19. Question: If a transportation problem has four origins and five destinations, the LP formulation of the problem will have
20. Question: For many waiting line situations, the arrivals occur randomly and independently of other arrivals and it has been found that a good description of the arrival pattern is provided by
21. Question: Modern revenue management systems maximize revenue potential for an organization by helping to manage
22. Question: Problem 12-27 (Algorithmic): Andalus Furniture Company has two manufacturing plants, one at Aynor and another at Spartanburg. The cost in dollars of producing a kitchen chair at each of the two plants is given here.

Aynor: Cost = 66Q1 + 6Q1² + 105

Spartanburg: Cost = 20Q2 + 2.5Q2² + 156

Where

Q1 = number of chairs produced at Aynor Q2= number of chairs produced at Spartanburg

Andalus needs to manufacture a total of 50 kitchen chairs to meet an order just received. How many chairs should be made at Aynor and how many should be made at Spartanburg in order to minimize total production cost? When required, round your answers to the nearest dollar.

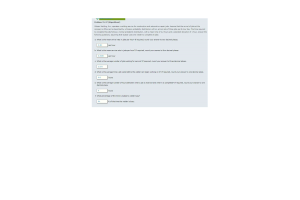
23. Question: The assignment problem constraint x₃₁ + x₃₂ + x₃₃ + x₃₄ ≤ 2 means
24. Question: The solution to the LP Relaxation of a maximization integer linear program provides
25. Question:  Problem 10-09 (Algorithmic): The Ace Manufacturing Company has orders for three similar products: Three machines are available for the manufacturing operations. All three machines can produce all the products at the same production rate. However, due to varying defect percentages of each product on each machine, the unit costs of the products vary depending on the machine used. Machine capacities for the next week and the unit costs are as follows: Use the transportation model to develop the minimum cost production schedule for the products and machines. Show the linear programming formulation. If required, round your answers to one decimal place. The linear programming formulation and optimal solution are shown.
26. Question: If the acceptance of project A is conditional on the acceptance of project B, and vice versa, the appropriate constraint to use is a
27. Question: Problem 11-9 (Algorithmic): Hawkins Manufacturing Company produces connecting rods for 4- and 6-cylinder automobile engines using the same production line. The cost required to set up the production line to produce the 4-cylinder connecting rods is $2200, and the cost required to set up the production line for the 6-cylinder connecting rods is $3700. Manufacturing costs are $16 for each 4-cylinder connecting rod and $18 for each 6-cylinder connecting rod. Hawkins makes a decision at the end of each week as to which product will be manufactured the following week. If there is a production changeover from one week to the next, the weekend is used to reconfigure the production line. Once the line has been set up, the weekly production capacities are 5900 6- cylinder connecting rods and 8500 4-cylinder connecting rods.

Let

x4 = the number of 4-cylinder connecting rods produced next week

x6 = the number of 6-cylinder connecting rods produced next week

s4= 1 if the production line is set up to produce the 4-cylinder connecting rods; 0 if otherwise

s6 = 1 if the production line is set up to produce the 6-cylinder connecting rods; 0 if otherwise

Using the decision variables x4 and s4, write a constraint that limits next week's production of the 4- cylinder connecting rods to either 0 or 8500 units.

Using the decision variables x₆ and s₆, write a constraint that limits next week's production of the 6- cylinder connecting rods to either 0 or 5900 units.

28. Question: Problem 9-15: Bay Oil produces two types of fuels (regular and super) by mixing three ingredients. The major distinguishing feature of the two products is the octane level required. Regular fuel must have a minimum octane level of 90 while super must have a level of at least 100. The cost per barrel, octane levels, and available amounts (in barrels) for the upcoming two-week period are shown in the following table. Likewise, the maximum demand for each end product and the revenue generated per barrel are shown.

Develop and solve a linear programming model to maximize contribution to profit. Let Ri = the number of barrels of input i to use to produce Regular, i=1,2,3

Si = the number of barrels of input i to use to produce Super, i=1,2,3

If required, round your answers to one decimal place. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300)

29. Question: Problem 15-7 (Algorithmic): Speedy Oil provides a single-server automobile oil change and lubrication service. Customers provide an arrival rate of 3.5 cars per hour. The service rate is 5 cars per hour. Assume that arrivals follow a Poisson probability distribution and that service times follow an exponential probability distribution.
30. Question: In a waiting line situation, arrivals occur, on average, every 10 minutes, and 10 units can be received every hour. What are λand μ?